朋友傳給我一個影片
我不太清楚出處
不過還滿有趣的
所以分享出來
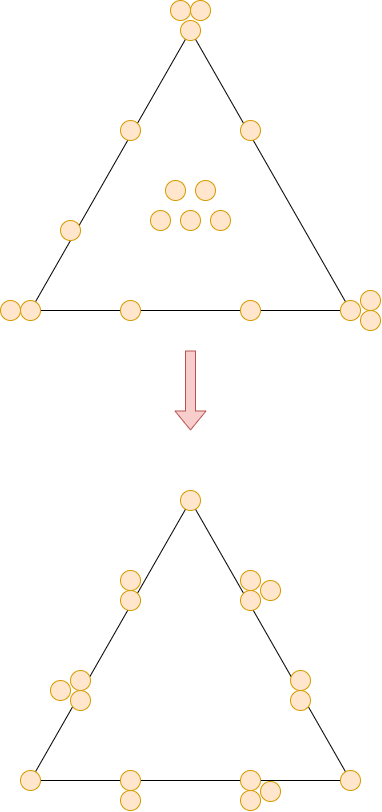
一開始將石頭分散擺成正方形
每個邊各有8顆石頭
而中心有6顆石頭

最後將中心的石頭都移到邊上
但每個邊仍舊只有8顆石頭
究竟是為什麼呢?

在影片的開頭
所有邊上的石頭共有22顆
但是每個邊要有8顆的話
照理要有 8 * 4 = 32 顆石頭
既然差了10顆
代表要有10顆石頭重複使用
而這10顆石頭就放在四個角上
因為一個角可以給兩個邊計算
在影片的末尾
中心6顆石頭都放到邊上
四個邊現在有 22 + 6 = 28 顆石頭
與32顆石頭差了4顆
既然只有4個重複
每個角只各放一顆石頭
因此實際的過程
除了把中心的石頭放到邊上
還要把角上的石頭放到邊中間
多了中心的石頭 +6
少了角上的石頭 -6
一來一往每個邊總數不變
仍舊只有8顆石頭
魔鬼就藏在角落裡!
知道背後原理後
我們也可以修改題目
只要確保
邊石頭量 * 邊數量 = 石頭總量 + 邊數量
例如三角形每邊7顆
7 * 3 = 18 + 3
是不是很有趣呢?